Agora que já sabemos a “caminhar” na reta numerada, iremos aprender as operações envolvendo números inteiros. Iniciaremos nossos estudos com adição e a subtração de números inteiros.

Adição

Iremos aprender a fazer a operação de soma com os números inteiros. Iremos usar a reta numerada para facilitar nosso aprendizado.

Partindo do ponto de abscissa 0, caminharemos inicialmente o que estiver indicado na primeira parcela e em seguida o que estiver indicado na segunda. Chegaremos a um número que é a soma dos números dados. É importante saber qual direção tomar, direita ou esquerda. Caminharemos para o direita, quando o número indicado for positivo e caminharemos para a esquerda, quando o número indicado for negativo.

1º caso: adição de números de mesmo sinal

A soma de dois números inteiros de mesmo sinal é obtida adicionando-se seus valores absolutos e conservando-se o sinal comum.

Exemplos:

a) (+4) + (+5)

Primeiro iniciaremos a nossa contagem partindo do ponto de abscissa 0, caminhamos quatro unidades para a direita e em seguida caminhamos mais cinco unidades para direita. Chegamos ao ponto de abscissa +9, ou seja 9:

Então: (+4) + (+5) = 9

b) (+2) + (+4)

Assim como no exemplo acima, iniciamos a nossa contagem partindo do ponto de abcissa 0, caminhamos para a direita duas unidades, em seguida caminhamos também para a direita quatro unidades. Chegamos ao ponto de abscissa +6, ou simplesmente 6:

Então: (+2) + (+4) = 6

c) (−5) + (−4)

Como nos exemplos anteriores, iniciamos a nossa contagem partindo do ponto de abscissa 0. Agora ao in vez de caminhar para a direita, iremos caminhar para a esquerda, pois o número (−5) é negativo. Caminharemos cinco unidades, em seguida caminharemos também para a esquerda quatro unidades. Chegaremos ao ponto −9:

Então: (−5) + (−4) = −9

d) (−1) + (−3)

Como você já foi dito, iniciaremos a nossa contagem partindo do ponto de abscissa 0. Agora caminharemos para a esquerda uma unidade, em seguida caminharemos também para a esquerda três unidades. Chegaremos ao ponto −4:

Então: (−1) + (−3) = −4

2º caso: Adição de números de sinais diferentes

A soma de dois números inteiros de sinais diferentes é obtida subtraindo-se seus valores absolutos, dando-se ao resultado o sinal do número de maior valor absoluto.

Exemplos:

a) (+9) + (−4)

Saindo do ponto de abscissa 0, caminharemos nove unidades para a direita. Em seguida caminharemos quatro unidades para a esquerda. Chegamos ao ponto de abscissa 5:

Então: (+9) + (−4) = 5

b) (+4) + (−3)

Saindo do ponto de abscissa 0, caminharemos quatro unidades para a direita. Em seguida caminharemos três unidades para a esquerda. Chegamos ao ponto de abscissa 1:

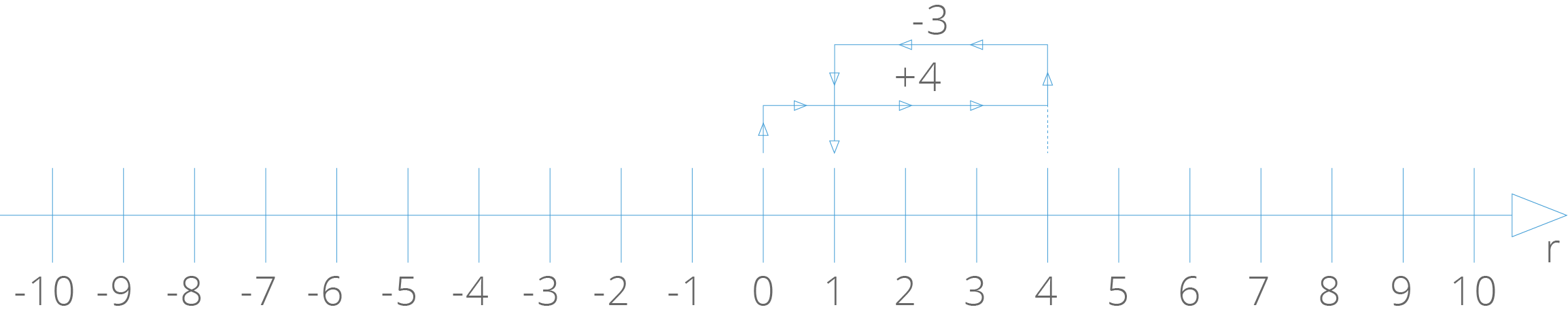
Então: (+4) + (−3) = 1

c) (−7) + (+3)

Saindo do ponto de abscissa 0, caminharemos sete unidades para a esquerda. Em seguida caminharemos três unidades para a direita. Chegamos ao ponto de abscissa −4:

Então: (−7) + (+3) = −4

d) (−5) + (+7)

Saindo do ponto de abscissa 0, caminharemos cinco unidades para a esquerda. Em seguida caminharemos sete unidades para a direita. Chegamos ao ponto de abscissa 2:

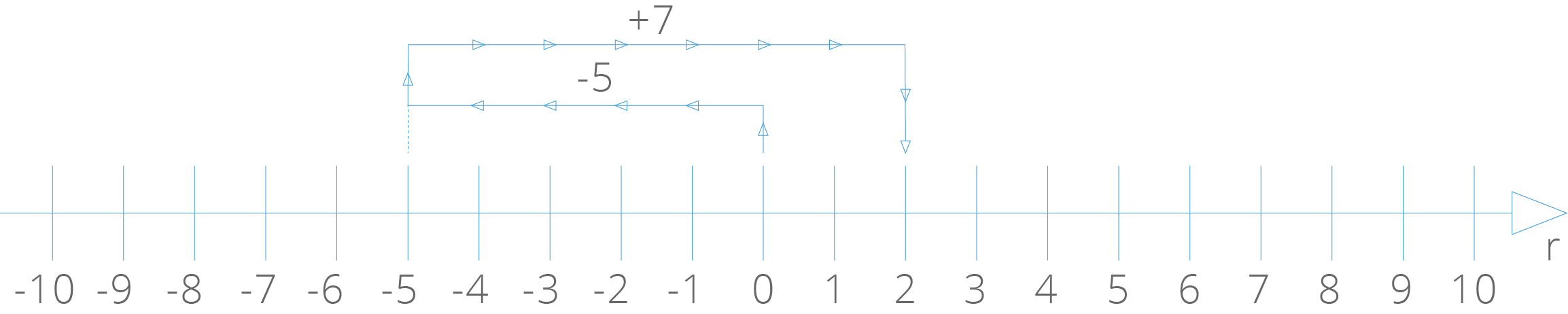
Então: (−5) + (+7) = 2

3º caso: Adição três ou mais parcelas

Para resolvermos uma adição com três  ou mais parcelas, podemos obter a solução de varias maneiras. Uma maneira é:

→ Começamos a resolver a sentença de esquerda para a direita, pegando as dois primeiras parcelas;

→ Com o resultado das duas primeiras parcelas, resolvemos com a próxima parcela;

→ Assim por diante, fazemos isso até acabar as parcelas.

Exemplo:  Efetue (+7) + (+8) + (−6) + (−1)

(+7) + (+8) + (−6) + (−1) =

= (+15) + (−6) + (−1) =

= (+9) + (−1) = = 8

Outra maneira para resolvermos uma adição com três  ou mais parcelas, bem mais simples é:

→ Somamos as parcelas positivas;

→ Somamos as parcelas negativas;

→ Somamos os resultados obtidos.

Exemplo: Efetue  (−7) + (−9) + (+2) + (+7) + (−1)

(−7) + (−9) + (+2) + (+7) + (−1) =

= (−17) + (+9) =

= −8

4º caso: Adição de números opostos

A soma de dois números opostos é igual a zero

Exemplos:

a) (+5 ) + (−5)

Saindo do ponto de abscissa 0, caminharemos cinco unidades para a esquerda. Em seguida caminharemos cinco unidades para a direita. Chegamos ao ponto de abscissa 0:

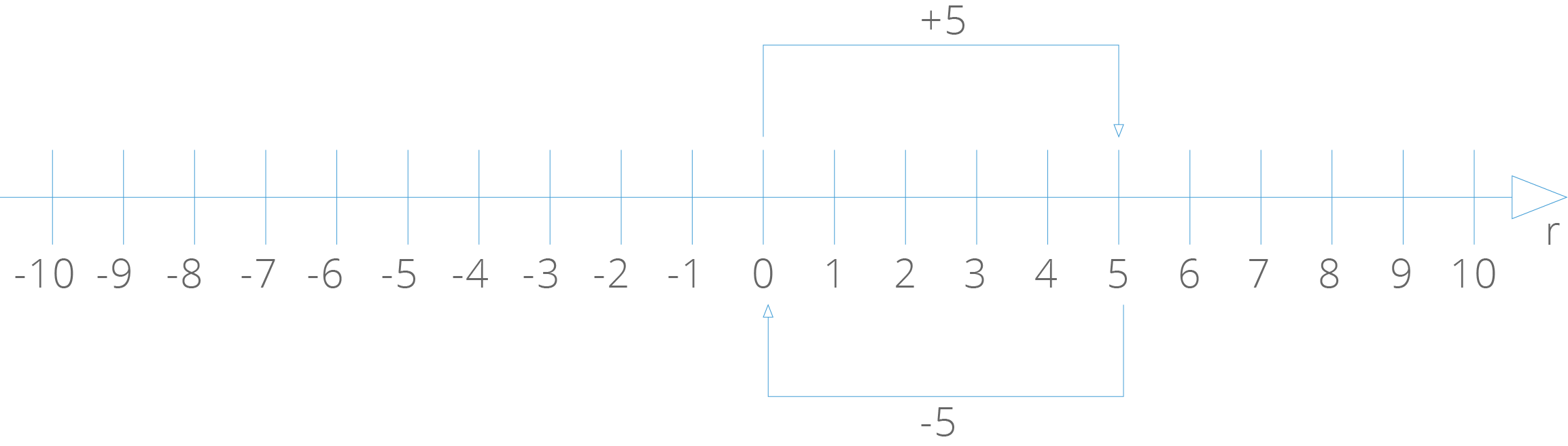
Então: (+5 ) + (−5) = 0

b) (−3) + (+3)

Saindo do ponto de abscissa 0, caminharemos três unidades para a direita. Em seguida caminharemos três unidades para a esquerda. Chegamos ao ponto de abscissa 0:

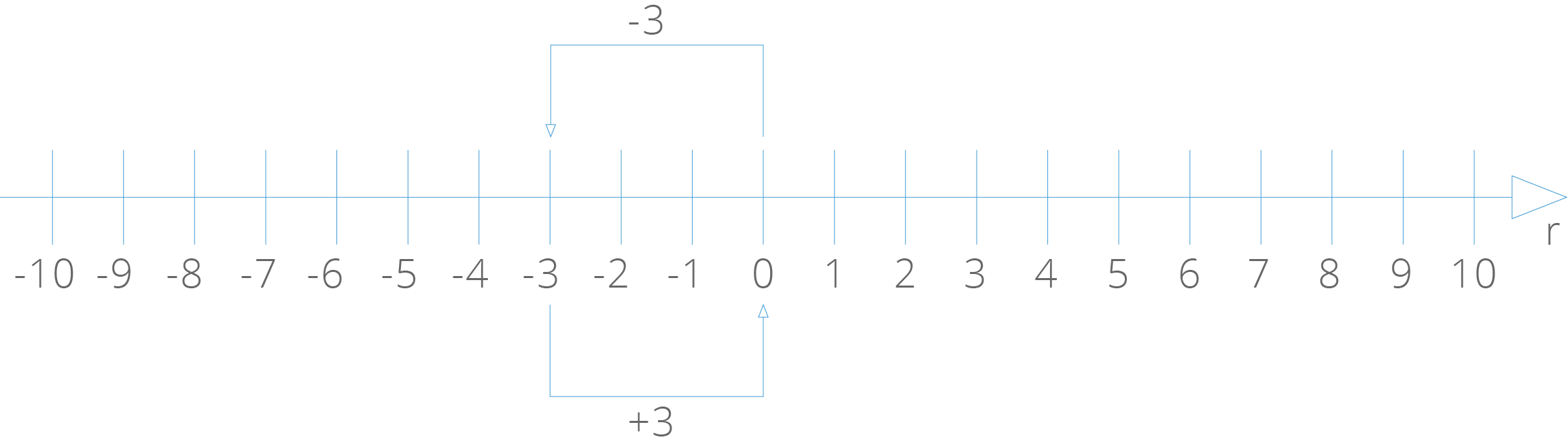
Então: (−3) + (+3) = 0

Propriedades da adição

A adição no conjunto dos números inteiros apresenta algumas propriedades estruturais, que veremos a seguir:

→ Propriedade comutativa da adição

Em uma adição de números inteiros a ordem das parcelas não altera a soma. De modo geral, se a ∈ Z e b ∈ Z, então:

a + b = b + a

Exemplos:

a) (+3) + (+2) = 5 ↔ (+2) + (+3) = 5

b) (−15) + (+9) = −6 ↔ (+9) + (−15) = −6

c) (+12) + (+10) = 22 ↔ (+10) + (+12) = 22

→ Propriedade do elemento neutro

O elemento neutro da adição é o número zero. De modo geral, se a ∈ Z, então:

a + 0 = 0 + a = a

Exemplos:

a) (+3) + (0) = 3 ↔ (0) + (+3) = 3

b) (+24) + (0) = 24 ↔ (0) + (+24) = 24

c) (−8) + (0) = −8 ↔ (0) + (−8) = −8

→ Propriedade associativa da adição

Em uma adição com três números inteiros, podemos associá-los diferentes, sem alterar o valor da soma. De modo geral, se a ∈ Z, b ∈ Z e c ∈ Z, então:

a + (b + c) = (a + b) + c

Exemplo:

a) (+7) + [(−3) + (+9)] = 13 ↔ [(+7) + (−3)] + (+9) = 13

b) (−5) + [(−4) + (−1)] = −10 ↔ [(−5) + (−4)] + (−1) = −10

c) (+9) + [(+16) + (−23)] = 2 ↔ [(+9) + (+16)] + (−23) = 2

→ Existência de elemento oposto ou simétrico

Todo número inteiro admite um número oposto ou simétrico a ele.  De modo geral, se a ∈ Z, então existe o elemento oposto (−a) tal que:

(+a) + (−a) = (−a) + (+a) = 0

Exemplo:

a) (+3) + (−3) = 0 ↔ (−3) + (+3) = 0

b) (+24) + (−24) = 0 ↔ (−24) + (+24) = 0

c) (+8) + (−8) = 0 ↔ (−8) + (+8) = 0

Subtração

Já sabemos, que a subtração é o inverso da adição.

Para calcularmos uma subtração, devemos procurar um número que somado com o subtraendo dê como resultado o minuendo. Para melhor compreensão, imaginemos a seguinte subtração: (+3) − (+5). Seguindo com a afirmação dita, devemos procurar um número que somado com o subtraendo, que no nosso caso é o +5 dê o resultado o minuendo, que no nosso caso é o +3. Iremos identificar esse número como a, então temos:

→ (+3) − (+5) = a ↔ a + (+5) = (+3) ou (+5) + a = (+3)

Veja na reta numerada abaixo que, partindo do zero e caminhando +5 unidades, precisamos voltar −2 unidades para chegarmos em +3. Veja:

Então, o valor de a é −2, ou seja: (+3) − (+5) = −2. Podemos afirmar que: (+3) − (+5) = (+3) + (−5).

De modo geral, se a e b forem dois números inteiros:

a − b = a + (−b)

Podemos afirmar que:

A diferença entre dois números inteiros é calculada adicionando-se o primeiro número ao oposto do segundo.

Vejamos outros exemplos aplicando essa regra:

a) (+6) − (+2) = (+6) + (−2) = 4

b) (−6) − (−2) = (−6) + (+2) = −4

c) (+6) − (−2) = (+6) + (+2) = 8

d) (−6) − (+2) = (−6) + (−2) = −8