Resolução de Equações

Resolver uma equação é determinar o seu conjunto verdade, considerando o conjunto universo dado. Para resolver uma equação, devemos reduzi-la à equação mais simples equivalente à equação dada. Para facilitar nesse processo, conheça agora algumas propriedades da igualdade:

Aplicação da Propriedade Aditiva

Observe alguns exemplos:

a) Seja a equação x – 3 = 5, em que V = {8}. Somando 3 aos dois membros dessa equação, temos:

x – 3 + 3 = 5 + 3

x + 0 = 5 + 3

x = 8

As equações x – 3 = 5, x + 0 = 5 + 3 e x = 8 têm o mesmo conjunto verdade e, portanto, são equivalentes.

b) Seja a equação x + 5 = 9, em que V = {4}. Somando –5 aos dois membros dessa equação, temos:

x + 5 – 5 = 9 – 5

x + 0 = 9 – 5

x = 4

As equações x + 5 = 9, x + 0 = 9 – 5 e x = 4 têm o mesmo conjunto verdade e, portanto, são equivalentes.

Com isso, mostramos que, aplicando a propriedade aditiva de uma igualdade, podemos transformar uma equação de 1º grau numa outra mais simples, equivalente a ela, e, dessa forma, obter a sua solução.

Veja alguns exemplos:

a) Determine o conjunto verdade da equação: x + 7 = 12 (U = Q)

Aplicando a propriedade aditiva, temos:

x = 12 – 7

x = 5

Logo, V = {5}.

b) Determine o conjunto verdade da equação: x – 17 = –9 (U = Q)

Aplicando a propriedade aditiva, temos:

x = –9 + 17

x = 8

Logo, V = {8}.

Aplicação da Propriedade Multiplicativa

Veja o seguinte exemplo:

Tomemos a equação 3x = 12, em que V = {4}, pois 3 × 4 = 12. Dividindo os dois membros dessa equação por 3, temos:

As equações 3x = 12 e x = 4 são equivalentes.

Assim, podemos afirmar que:

Dividindo os dois membros de uma equação por um número diferente de zero, obtemos uma equação equivalente à equação dada.

Vamos agora resolver algumas equações, sendo U = Q:

Veja o seguinte exemplo:

Seja a equação $ \frac{2x}{3} = \frac{12}{3} $, em que V = {6}, pois $ \frac{2 \times 6}{3} = \frac{12}{3} $. Multiplicando os dois membros dessa equação por 3 (o que é o denominador comum das frações), temos:

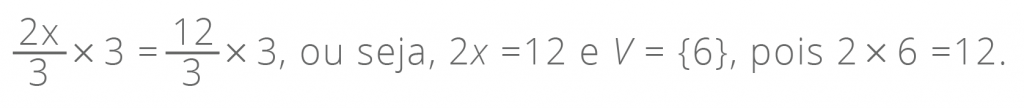
As equações $ \frac{2x}{3} = \frac{12}{3} $ e $ 2x = 12 $ são equivalentes.

Assim, podemos estabelecer que:

Quando todos os termos de uma equação têm o mesmo denominador, este pode ser cancelado multiplicando os dois membros dessa equação por esse denominador, e a nova equação assim obtida é equivalente à equação dada.

Agora, veja alguns exemplos:

a) $ \frac{5x}{7} = \frac{20}{7} $

Multiplicando os dois membros por 7, cancelaremos os denominadores:

$ 5x = 20 $

Dividindo os dois membros por 5, temos:

$ \frac{5x}{5} = \frac{20}{5} $, ou seja, x = 4

Logo, V = {4}.

b) $ \frac{2x}{5} = -\frac{7}{5} $

Multiplicando os dois membros por 5, cancelaremos os denominadores:

$ 2x = -7 $

Dividindo os dois membros por 2, temos:

$ \frac{2x}{2} = -\frac{7}{2} $, ou seja, $ x = -\frac{7}{2} $

Logo, V = {$ -\frac{7}{2} $}

c) $ \frac{x}{2} = \frac{5}{3} $

Nesse caso, os denominadores são diferentes. Para resolver essa equação, basta reduzir as frações ao mesmo denominador comum, o mmc. O mmc de (2,3) = 6:

$ \frac{3x}{6} = \frac{10}{6} $

Cancelando os denominadores, fica:

$ 3x = 10 $

Dividimos os dois membros por 3:

$ \frac{3x}{3} = \frac{10}{3} $, ou seja, $ x = \frac{10}{3} $

Logo, V = {$ \frac{10}{3} $}

Veja o seguinte exemplo:

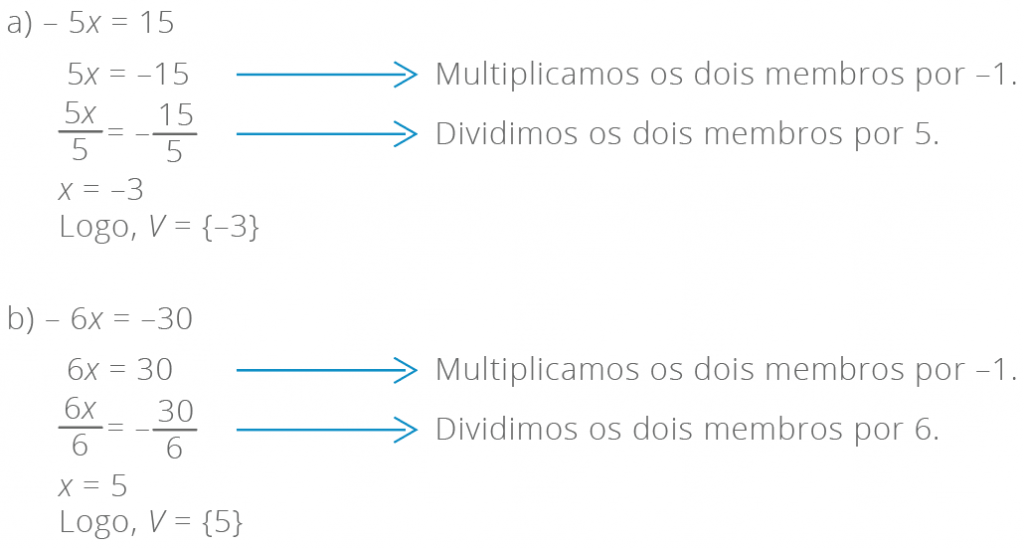
Considere a equação –2x = 12, em que V = {–6}, pois –2 × (–6) = 12. Multiplicando os dois membros dessa equação por –1, temos:

2x = 12 e V = {–6}, pois –2 × (–6) = –12

As equações –2x = 12 e 2x = –12 são equivalentes.

O exemplo nos mostra que:

Podemos trocar os sinais de todos os termos de uma equação, pois isso equivale a multiplicar os dois membros da equação por –1

Vamos agora resolver algumas equações, sendo U = Q: