Nos temas anteriores, aprendemos a realizar operações com nos números racionais absolutos. Também aprendemos as regras de sinais de operações no conjunto dos números inteiros.

Agora iremos aprender a realizar operações com números racionais relativos, usaremos as mesmas regras dos temas mencionados acima.

Adição de Números Racionais

Observe a forma de efetuar as seguintes regras:

Subtração de Números Racionais

Veja os exemplos:

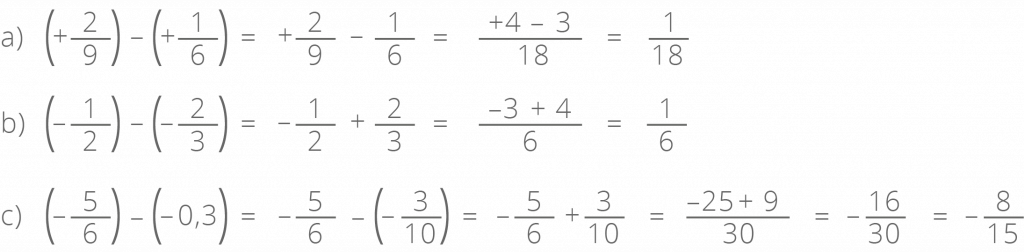
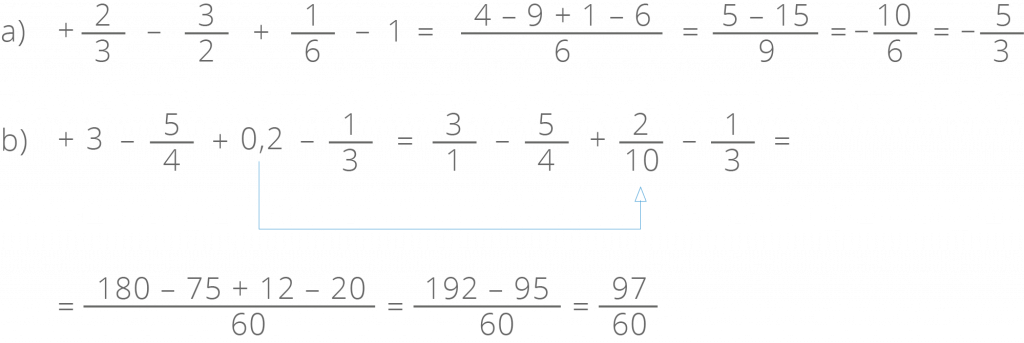
Adição Algébrica de Números Racionais

Lembrando que a adição algébrica é toda expressão onde aparecem apenas as operações de adição e subtração.

veja alguns exemplos:

Multiplicação de Números Racionais

Vamos recordar algumas teorias já estudadas:

→ Para calcular o produto entre números fracionários, multiplicamos o numerador entre si e o denominador entre si.

→ A regra de sinal para a multiplicação entre dois fatores é:

»Se os fatores tiverem o mesmo sinal, o produto será positivo;

»Se os fatores tiverem sinais diferentes, o produto será negativo.

Veja alguns exemplos:

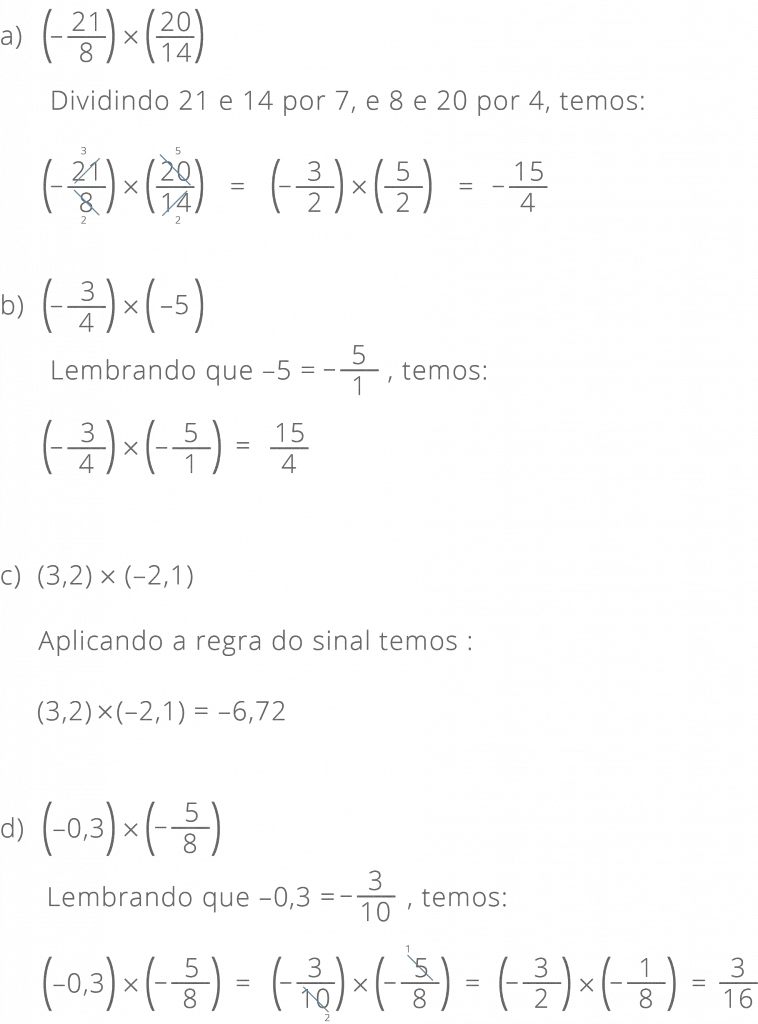
Propriedade da Adição e Multiplicação de Números Racionais

Veja as propriedades estruturais da adição e multiplicação dos números racionais:

→ Adição

» Comutativa

Se a ∈ Q e b ∈ Q, então:

a + b = b + a

» Elemento neutro

Se a ∈ Q, então:

a + 0 = 0 + a = a

» Associativa

Se a, b e c ∈ Q, então:

(a + b) + c = a + (b + c)

» Elemento oposto

Se a ∈ Q, então:

a + (−a) = (−a + a) = 0

→ Multiplicação

» Comutativa

Se a ∈ Q e b ∈ Q, então:

a × b = b × a

» Elemento neutro

Se a ∈ Q, então:

a × 1 = 1 × a = a

» Associativa

Se a, b e c ∈ Q, então:

(a × b) × c = a × (b × c)

» Elemento inverso

Se a ∈ Q*, então:

→ Distributiva da multiplicação em relação à adição

Se a, b, c ∈ Q, então:

a × (b + c) = a × b + a × c

Pela importância que a propriedade distributiva da multiplicação tem no curso de matemática do 1º grau, vamos, como exemplo, aplicá-la nas seguintes expressões:

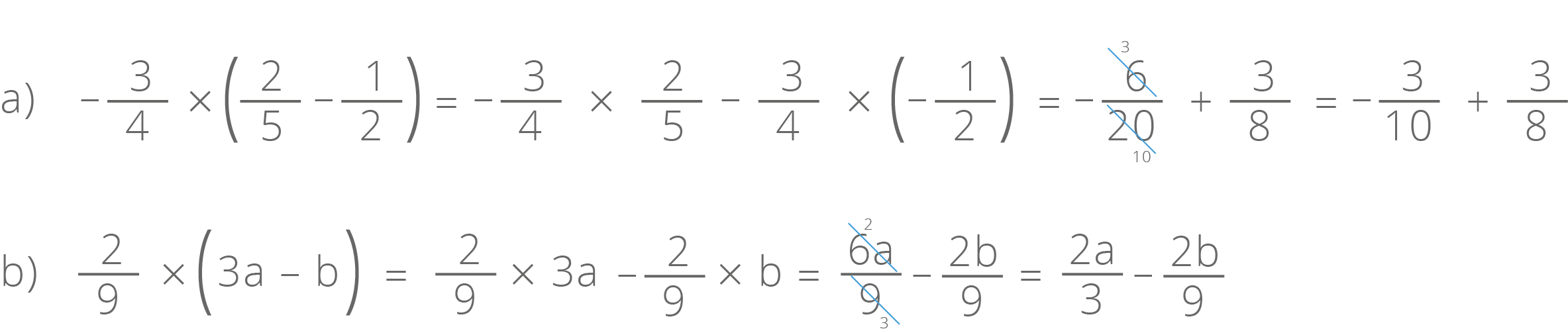
Divisão de números racionais

Lembrando que para calcular uma divisão de frações, basta multiplicar a primeira fração pelo inverso da segunda fração.

Veja alguns exemplos:

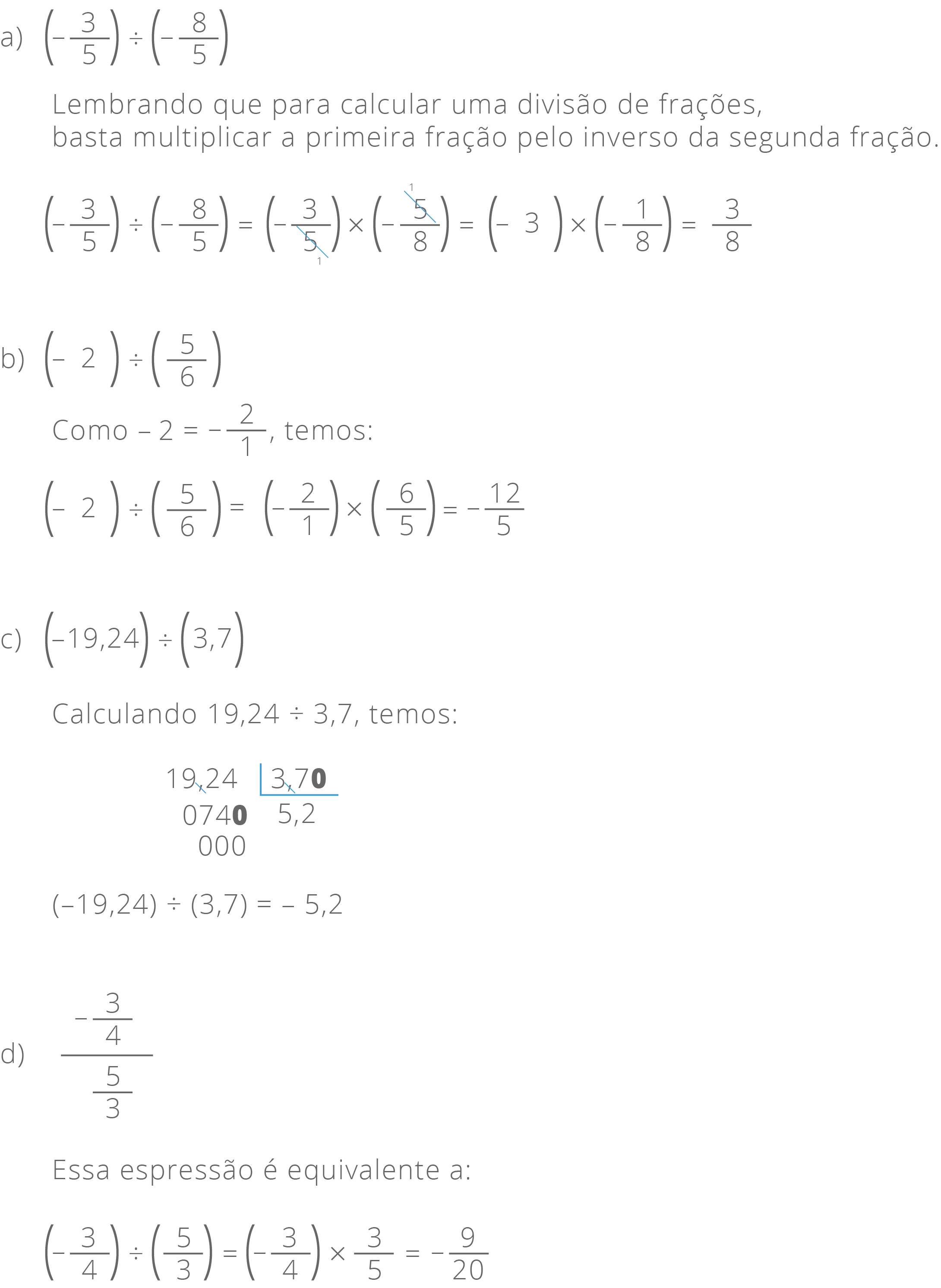
Potenciação de números racionais

Considerando os estudos anteriores, iremos calcular agora potências que tenham como base um número racional (positivo ou negativo) e como expoente um número natural.

→ Toda potência com expoente 0 é igual a 1.

→ Toda potência com expoente 1 é igual à própria base.

→ Toda potência com expoente maior que 1 é igual a um produto onde o número de fatores é igual ao expoente da potência e todos os fatores são iguais à base.

Exemplos:

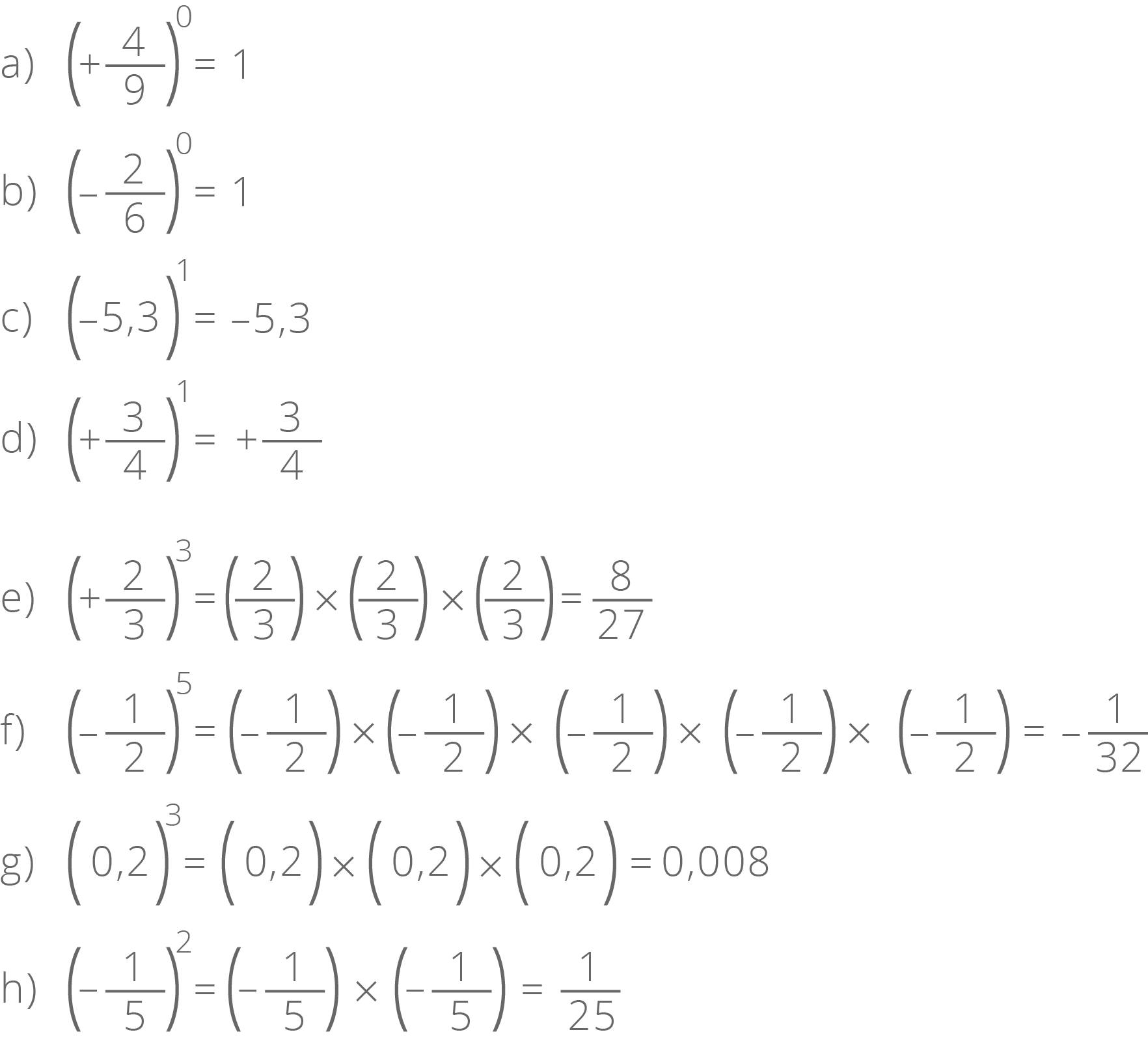
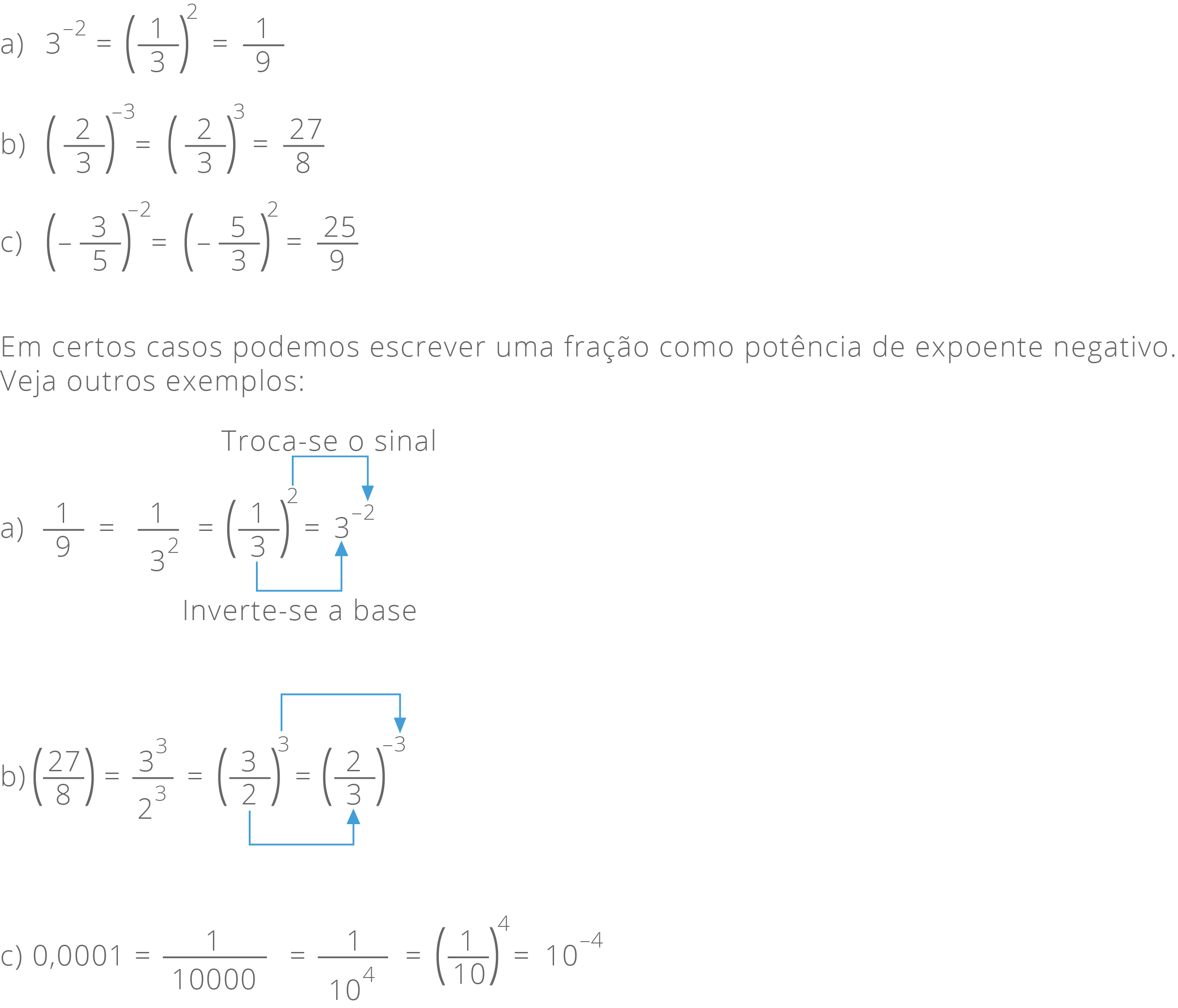
Potência com expoente inteiro negativo

Já aprendemos a realizar operações com potências que têm na base um número racional e por expoente um número natural. Agora iremos aprender a realizar operações com potência que tenha expoente um número inteiro negativo.

Considere o seguinte quociente 5² ÷ 5⁵. Pela propriedade do quociente de potência de mesma base, temos:

conforme vimos no exemplo acima, podemos afirmar que:

A potência com expoente negativo de um número racional diferente de zero é igual a uma outra potência que tem a base igual ao inverso da base anterior e o expoente igual ao oposto do expoente anterior.

Como exemplo, vamos calcular:

Propriedade da potenciação

As propriedades das potências do conjunto Z valem também para o conjuntos Q.

Vamos recordar:

1ª propriedade: produto de potências de mesma base

Para reduzir um produto de potências de mesma base a uma só potência, conservamos a base e somamos os expoentes.

2ª propriedade: quociente de potências de mesma base

Para reduzir um quociente de potência de mesma base a uma só potência, conservamos a base e subtraímos os expoentes.

3ª propriedade: potência de potência

Para reduzir uma potência de potência a uma potência de um só expoente, conservamos a base e multiplicamos os expoentes.

Veja alguns exemplos:

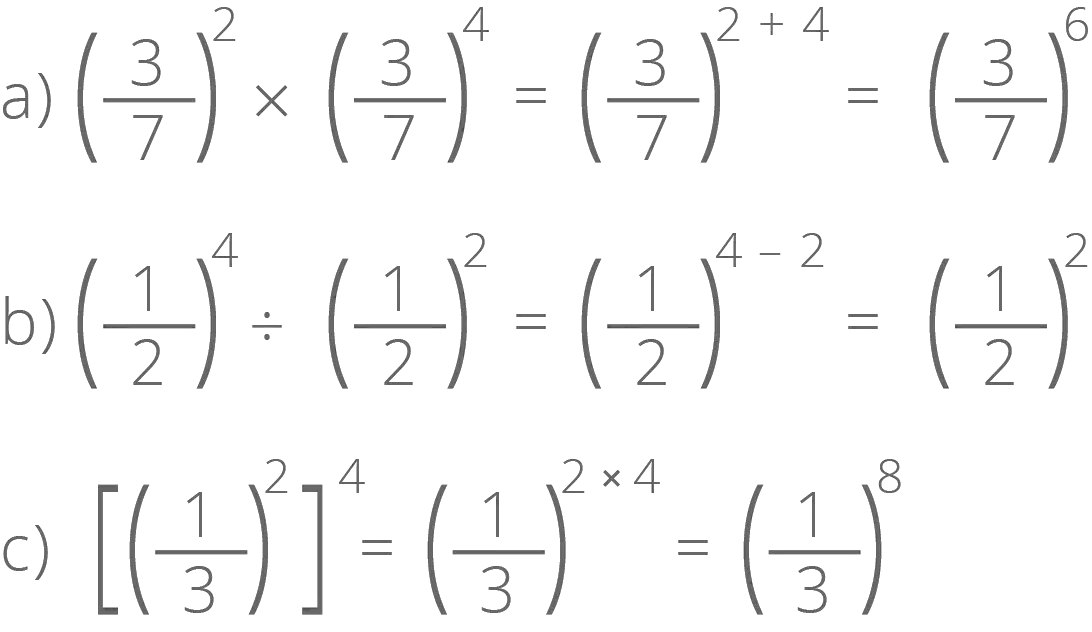
Raiz quadrada de números racionais

A raiz quadrada de um número racional positiva quadrado perfeito é um número racional positivo.

Exemplos:

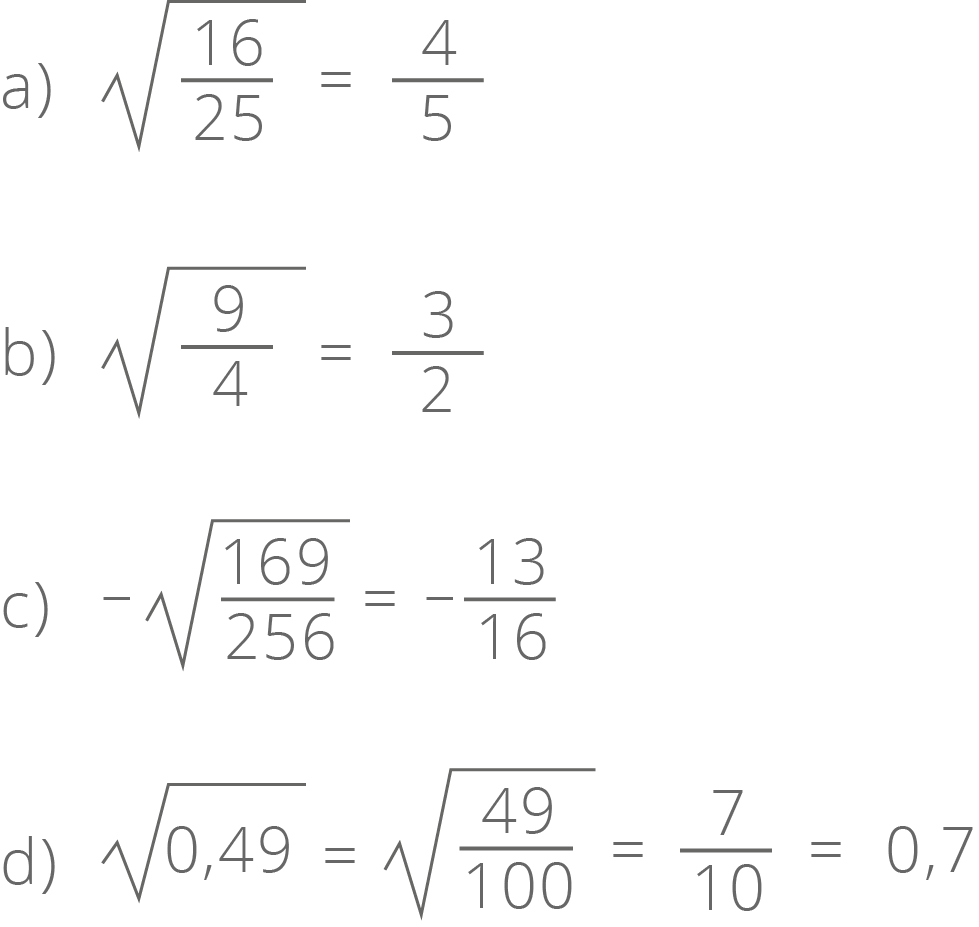
É importante saber:

→ Um número racional, quando elevado ao quadrado, dá o número zero ou um número racional positivo. Logo, os números racionais negativos não tem raiz quadrada em Q.

→ Um número racional positivo só tem raiz quadrada no conjunto dos números racionais se ele for um quadrado perfeito.