Quando duas ou mais frações têm denominadores diferentes, é possível transformá-las em outras frações equivalentes que tenham denominadores iguais. A isso chamamos redução de frações ao mesmo denominador.

Como exemplo, vamos reduzir ao mesmo denominador as frações \(\frac{2}{3}, \frac{3}{4}\) e \(\frac{5}{6}\). Para isso, basta multiplicarmos os termos de cada fração por um número natural conveniente. Assim, temos:

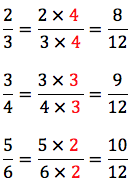
As frações \(\frac{2}{3}, \frac{3}{4}\) e \(\frac{5}{6}\) são, respectivamente, equivalentes às frações \(\frac{8}{12}, \frac{9}{12}\) e \(\frac{10}{12}\), que têm denominadores iguais:

Na prática, essas reduções são feitas da seguinte maneira:

• Calcula-se o mmc dos denominadores: \(\text{mmc}(3, 4 \text{ e } 6) = 12\)
• Divide-se o mmc pelos denominadores das frações dadas: \(12 \div 3 = 4\), \(12 \div 4 = 3\) e \(12 \div 6 = 2\)
• Multiplicam-se esses quocientes pelos respectivos numeradores:

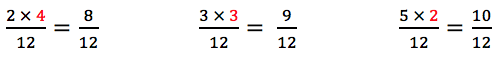
Vejamos outro exemplo:

Reduzir ao mesmo denominador: \(3\frac{1}{2}, \frac{3}{5}, 2, \frac{11}{10}\)

Escrevemos \(3\frac{1}{2} = \frac{7}{2}\) e \(2 = \frac{2}{1}\), as frações a serem reduzidas ao mesmo denominador ficam assim:

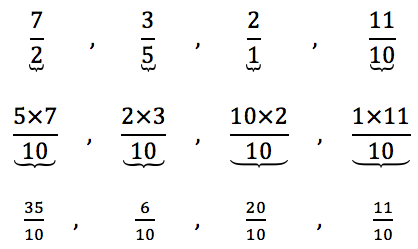
mmc(2, 5, 1, 10) = 10

Frações equivalentes às frações dadas com denominadores iguais: